With Very Few Degrees of Freedom the Test Statistic

Therefore it has two values for the degrees of freedom. Should be a z test rather than a t test.

Degrees Of Freedom In Statistics Statistics By Jim

This is because in order to understand the importance of a chi-square statistic and whether or.

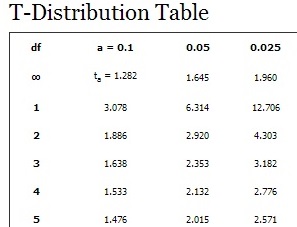
. T-statistic and degrees of freedom. Published on July 17 2020 by Rebecca BevansRevised on August 2 2021. A sM 229.

QUESTION 12 For which of the following test statistics do you NOT use degrees of freedom when determining critical value. O employed should be a 2 test rather than a r test. 5 out of 5 points With very few degrees of freedom the test statistic.

Needs to be less extreme to reject the null hypothesis. With very few degrees of freedom the test statistic. The F distribution is the ratio of two sample variances.

D employed should be a z test rather than a t test. In statistics the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Where x is the sample mean μ is the hypothesized mean s is the sample standard deviation n is the sample size and df is the degrees of freedom.

A needs to be less extreme to reject the null hypothesis. Used should be a z test rather than a t test. The number of independent ways by which a dynamic system can move without violating any constraint imposed on it is called number of degrees of freedom.

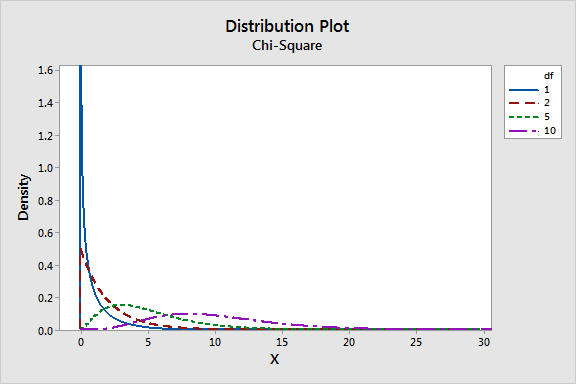
Needs to be more extreme to reject the null hypothesis. The tails consist of the extreme values of the distribution both negative and positive Eventually when the degrees of freedom reaches 30 or more the t-distribution and the standard normal distribution are. O dfx dfy.

Needs to be less extreme to reject the null hypothesis. Defining Degrees of Freedom. Needs to be more extreme to reject the null hypothesis.

C becomes more reliable. A statistic is an estimate of the corresponding property in the population or process from which the sample was drawn. Needs to be more extreme to reject the null hypothesis.

Becomes more reliable b. Needs to be more extreme to reject the null hypothesis. Needs to be more extreme to reject the null hypothesis d.

The formula for the degrees of freedom for the single-sample t test is. With very few degrees of freedom the test statistic needs to be more extreme to reject the null hypothesis. Therefore the test statistic is.

The F-test statistic is the ratio after scaling by the degrees of freedom. Or QUESTION 13 What is the probability of two randomly selected people being born on the same day of the week. Degrees of freedom refer to the number of values in a study that are free to vary.

B needs to be more extreme to reject the null hypothesis. Needs to be less extreme to reject the null hypothesis. Youve probably heard the term degrees of freedom thrown around while discussing the various forms of hypothesis testing that exist such as a chi-square.

With very few degrees of freedom the test statistic. If there is no difference between population means this ratio follows an F -distribution with 2. In other words the number of degrees of freedom can be defined as the minimum number of.

It shows how closely your observed data match the distribution expected under the null hypothesis of that statistical test. D should be a z test rather than a t test. B becomes more reliable.

As it says at the Wikipedia article there the test statistic 2 log. B needs to be more extreme to reject the null hypothesis. Needs to be more extreme to reject the null hypothesis.

Should be a z test rather than a t test c. Below you will find descriptions and details for the 1 formula that is used to compute the t-statistic and degrees of freedom for a Student t-test. Should be a z test rather than a t test.

For any given study always try to test more subjects to increase precision ie. The z-test statistic has only one probability distribution the standard normal distribution. C needs to be less extreme to reject the null hypothesis.

One associated with the numerator and the other one associated with. As the degrees of freedom increases the area in the tails of the t-distribution decreases while the area near the center increases. With very few degrees of freedom the test statistic.

95 CI of the estimate. 38 39 Question 13 5 out of 5 points With very few degrees of freedom the test statistic. Λ for a nested model will be asymptotically chi-squared distributed χ 2 with degrees of freedom equal to the difference in dimensionality of Θ and Θ 0 when H 0 holds true.

A statistic is a numerical property of a sample for example the sample mean or sample variance. The test statistic is a number calculated from a statistical test of a hypothesis. With very few degrees of freedom the test statistic.

Degrees of freedom refers to the number of pieces of information that are available and are determined by sample size. P 12 p 114 p17 p277 p 149 QUESTION 16 A statistical study resulted in a test statistic in the critical region. From the information the F-test with five degrees of freedom in the numerator and seven degrees of freedom in the denominator produced a test statistic whose value is 746.

T distributions with more degrees of freedom approximate the Normal distribution more closely. Needs to be more extreme to reject the null hypothesis. Test statistics Definition Interpretation and Examples.

With very few degrees of freedom the test statistic a needs to be more extreme to reject the null hypothesis. Needs to be less extreme to reject the null hypothesis. Needs to be less extreme to reject the null hypothesis.

Degrees Of Freedom In Statistics Statistics By Jim

Degrees Of Freedom Definition

Degrees Of Freedom What Are They Statistics How To